Solving Games: A Third Method

So far we have used the dominant strategy solution and iterative elimination of dominated strategy (IEDS) solution concepts to solve strategic form games.  A third approach is to use the Nash equilibrium concept.

If strategy b is dominated by strategy a, then one should never play b. But suppose there are circumstances in which c does not dominate d, except when your opponent picks a particular strategy.  If you and your opponent can anticipate each others' moves, then there may be a solution to the game that you couldn't find using dominant strategies or IEDS.

Some definitions:

Conjecture

Best response

Nash Equilibrium Necessary requirements for a Nash equilibrium are that each player play a best response against a conjecture, and the conjecture must be correct.

Intuition and Nash equilibrium: Different ways of conceiving of a Nash equilibrium.

For a given game you advise Elmer and Bugs on what strategy to play.  Once they have heard your prescription they see that no other strategy would make either of them better off.

If the players in a prisoners' dilemma could communicate before being interrogated then they would surely agree to play a strategy other than the dominant one in which they both confess and go to jail.

Rational introspection entails each player pondering the expected outcome of a game.

A particular strategy vector may be a focal point in that it is a best response strategy for each player.

How do we identify the Nash equilibria in a game?

• Look for the dominant strategy.
  
• Eliminate the dominated strategies.
  
• Play a minimax strategy. In a zero sum game you choose that strategy in which your opponent can do you the least harm from among all of the 'bad' outcomes.
  
• Cell-by-cell inspection or trial and error. This is really an implementation of the 'best response'. Another look at best response, Oscar and Felix keep house.

Two questions about the Nash equilibrium

• Existence
  
• Uniqueness

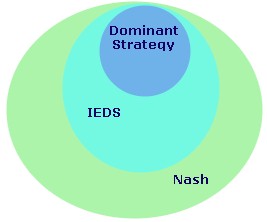
The relationship between the three solution methods:

The set of all possible games is enclosed in the box.  The colored circles are sets of game solutions identified by their respective solution methods.

• If there is a dominant strategy solution then that solution is also an IEDS solution and a Nash equilibrium. 
• If there is an IEDS solution, then it is also a Nash equilibrium.  Note that dominant strategy solutions are a proper subset of IEDS solutions. Even when there is no dominant strategy solution, there may be an IEDS solution.
• Even when there are no dominant strategy or IEDS solutions, there may be a Nash equilibrium.