Econometrics

Was Bread Giffin?

The budget data presented in the file BreadMeat.dat are taken from two studies of the standard of living of the English rural laborer conducted during the period 1787-1795 by the Reverend David Davies (The Case of Labourers in Husbandry (Bath, 1795) and Frederick Morton Eden (The State of the Poor (London, 1797)). According to Roger Koenker these were the seminal studies in that long and honorable liberal avocation - - snooping into the lives of the poor. By the 19^th century such studies were being conducted all over Europe by such well know gents as Ernst Engel, Friederich Engels, Frederic LePlay, and others. An introduction to these yoemen practitioners of the dismal science may be found in George Stigler's essay, "The Early History of Empirical Studies of Consumer Behavior", which has been reprinted in his Essays in the History of Economics.

The years 1787-1795 proved extremely difficult for the laboring classes of Britain. As the level of economic activity declined in the period leading up to Britain's entry into the Napoleanic Wars in 1793, unemployment rose sharply, especially in rural areas, and the "price of provisions" rose even more dramatically. Hence, in contrast to later budget studies, the Davies-Eden budgets explicitly report large differences in commodity prices between localities and over time. Thus, we are presented with a unique opportunity to estimate demand functions from budget data on households.

Background reading should include Roger Koenker, Review of Economics and Statistics, 1977 and Henderson and Quandt, Microeconomic Theory, 2^nd edition, McGraw-Hill, Pp. 27-36, 1971. Any good microeconomic theory text will treat the relationship between the Slutsky equation and the elasticities of demand if you cannot find H&Q. If you don't have the time for the requisite reading in H&Q, then use these hints.

Question 1: Estimate two demand for bread equations:
(1.a)
and
(1.b)
where Y is income, S is family size, P_B is the price of bread and P_M is the price of meat.

Question 2: In the first, only income matters model, test the null hypothesis that the Engel curve for bread is homogeneous against the alternative that families have some committed quantity of bread which they will purchase regardless of family income.

Question 3: In the second model, test the following hypotheses:

Question 3.a. Family size and bread and meat prices are not significant influences on bread consumption.

Question 3.b. Conditional on your rejection of the above hypothesis, test whether or not the price of meat is a significant factor in determining bread consumption.

Question 4. One problem with linear models such as those proposed in question 1 is that the interpretation of te estimated parameters is intimately connected with the units of measurement of the included variables (when weekly income rises by 10 pence, average family bread consumption rises by 10 half-peck loaves per week (a half-peck loaf is, by the way, the amount of bread that can be made with a bit less than a half-peck of wheaten flour (about 8 lbs. 11 ozs. of bread))). For readers not attuned to such esoterica it is often convenient to present estimates of elasticities of demand with respect to income or price. But since the relationship that has been estimated is linear, the values taken by these elasticities will depend on the values taken by Q_B, Y, S, P_B, and P_M. The usual practice in such circumstances is to discuss elasticities evaluated at the sample means. Calculate the following based on your estimates of the second model (1.b):
Q.4.1. The income elasticity of bread consumption
Q.4.2. The uncompensated own price elasticity of bread consumption
Q.4.3. The compensated own price elasticity of bread consumption
Q.4.4. The compensated cross (meat) price elasticity of bread consumption
What do these estimates mean and are they reasonable?

Question 5. Estimate the demand for meat equation

and test the hypotheses:
Q.5.1. Meat is a luxury good. Recall this means that it has income elasticity greater than one, so evaluating at the sample means the hypothesis is

Q.5.2. Meat and bread are substitutes. This is easily done by testing

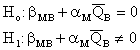
Question 6. Estimate the demand equations in log form:

What interpretation do the coefficients have in these equations? Test the hypotheses:

Q.6.1 If family size and income both increase by the same proportion, then bread consumption increases by the same proportion too.

Q.6.2. Same as Q.6.1., but for meat consumption.

Notes on the accompanying data set called BreadMeat.dat

Expenditures (price times quantity) per week on bread and meat are in old pence. The price of bread is in old pence per half peck loaf. The price of meat is in old pence per pound of bacon. When a household purchased flour, an equivalent quantity of bread was computed. In cases where consumption of meat was not in the form of bacon an equivalent quantity of bacon was computed.

This problem set was written by Roger Koenker of the University of Illinois. It was assigned to me when I was a graduate student there. I liked it so much that I have used it for many years at Temple University.