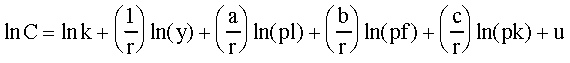
Multiple Regression
This is an example of multiple regression. It is taken from Ernst Berndt, The
Practice of Econometrics: Classic and Contemporary, Addison Wesley, Reading, MA:1991.
The specific problem is Exercise 3-4. The entirety of the chapter is worth reading. The
object of the exercise is to replicate Marc Nerlove's classic work on scale economies
("Returns to Scale in Electricity Supply," Chapter 7 in C.F. Christ, ed., Measurement
in Economics, Stanford, Calif., Stanford University Press, pp. 167-198).
To set the stage, consider the following presentation on factor price frontiers.
The model being estimated is
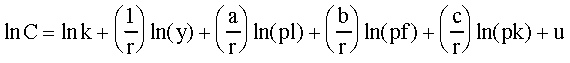
We will impose the restriction that the cost frontier be homogeneous of degree 1 in prices. Making this substitution and doing a bit of algebra yields:
with the happy result that . Thus we can see if there are constant
returns to scale by inverting the coefficient on output. A definitive conclusion would be
contingent on a test of hypothesis.
The code which follows, in red, is a LimDep program that reads a data file, estimates a
regression model and produces some descriptive statistics. The data file is called Nerlove and can be accessed by clicking here or going to the homework and data sets section of the course web. If
you were so inclined, you could download the data and try this on your own. The LimDep
program is illustrative of how you would use the data in most other software packages.
? Chapter 3 Exercise 4
READ ; NREC = 145 ; NVAR = 6; NAMES = 1 ; FILE=A:NERLOV $
? Part (a)
CREATE ; LNCP3 = LOG(COSTS/PF)
; LNP13 = LOG(PL/PF)
; LNP23 = LOG(PK/PF)
; LNKWH = LOG(KWH) $
? Part (b)
CRMODEL ; LHS = LNCP3 ; RHS = ONE,LNKWH,LNP13,LNP23
; RES = COSTRES $
? Part (e)
PLOT ; LHS = LNKWH ; RHS = COSTRES $
DSTATS ; RHS = LNKWH,COSTRES ; OUTPUT = 3 $
The output from this regression model follows:
Ordinary least squares regression. Dep. Variable = LNCP3 Observations = 145 Weights = ONE Mean of LHS = -0.1484195E+01 Std.Dev of LHS = 0.1482087E+01 StdDev of residuals= 0.3917620E+00 Sum of squares = 0.2164032E+02 R-squared = 0.9315846E+00 Adjusted R-squared= 0.9301290E+00 F[ 3, 141] = 0.6399802E+03 Log-likelihood = -0.6783837E+02 Restr.(á=0) Log-l = -0.2622948E+03 Amemiya Pr. Criter.= 0.9908741E+00 Akaike Info.Crit. = 0.1577113E+00 ANOVA Source Variation Degrees of Freedom Mean Square Regression 0.2946676E+03 3. 0.9822253E+02 Residual 0.2164032E+02 141. 0.1534775E+00 Total 0.3163079E+03 144. 0.2196583E+01 Durbin-Watson stat.= 1.0153695 Autocorrelation = 0.4923152 Variable Coefficient Std. Error t-ratio Prob|t|>x Mean of X Std.Dev.of X ------------------------------------------------------------------------------- Constant -4.6908 0.8849 -5.301 0.00000 LNKWH 0.72069 0.1744E-01 41.334 0.00000 6.5567 1.9128 LNP13 0.59291 0.2046 2.898 0.00435 -2.5372 0.33858 LNP23 -0.73811E-02 0.1907 -0.039 0.96919 1.9479 0.35980
To test the hypothesis that there are constant returns to scale construct the usual
test statistic 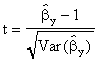
t = -16.01. Apparently there are increasing returns to scale.
There seems to be a small problem with these results. The implied estimates for exponents in the production function are a = (.72069*.59291) = .43 and c = (.72069*-.00738) = -.005. This latter estimate implies a negative marginal product for capital, clearly an undesirable result.
MODEL COMMAND: PLOT;LHS=LNKWH;RHS=COSTRES$

From the scattergram it appears that there is a u-shaped relationship between the residuals and output. Is this due to heteroscedasticity?
Also, go back and take a look at the Durbin-Watson statistic. Without getting into details, the DW statistic should be close to 2 in a statistical sense. It is also conventionally applied in time series data. Nevertheless, the observed value of 1.01 is quite small. The data was arranged by firm size so one might conclude that the DW serves as a measure of the correlation between firms of similar size.
A third possibility is that the scattergram and DW statistic suggest that the model has been misspecified.
It was Nerlove's supposition that the distinctive scattergram and low DW caused by differing returns to scale for firms in different class sizes.
MODEL COMMAND:
DSTATS;RHS=LNKWH,COSTRES;OUTPUT=3$
Descriptive Statistics
Variable Mean Std. Dev. Skew. Kurt. Minimum Maximum Cases
LNKWH 6.5567 1.9128 -0.958 3.627 0.6931 9.724 145
COSTRES -0.30348E-09 0.38766 1.247 7.564 -1.012 1.819 145
Covariance Matrix
1-LNKWH 2-COSTRES
1-LNKWH 3.6588
2-COSTRES 0.18204E-08 0.15028
Correlation Matrix
1-LNKWH 2-COSTRES
1-LNKWH 1.0000
2-COSTRES 0.24550E-08 1.0000
Although there is clearly a connection between the cost residuals and output, it is not linear. This explains why the correlation between the two variables is so small.
To explore the possibility of returns to scale varying by firm size we will estimate a model for each of five size classes, then a model in which the price coefficients are constrained to be equal but the output coefficient and intercept can differ, and a single model that is quadratic in the output variable. The final model is another way to permit returns to scale to vary with firm size.
? Chapter 3 Exercise 5
READ ; NREC = 145 ; NVAR = 6
; NAMES = 1 ; FILE=A:NERLOV $
? Part (a)
CREATE ; LNCP3 = LOG(COSTS/PF)
; LNP13 = LOG(PL/PF)
; LNP23 = LOG(PK/PF)
; LNKWH = LOG(KWH) $
SAMPLE ; 1-29 $
CRMODEL ; LHS = LNCP3 ; RHS = ONE,LNKWH,LNP13,LNP23 $
SAMPLE ; 30-58 $
CRMODEL ; LHS = LNCP3 ; RHS = ONE,LNKWH,LNP13,LNP23 $
SAMPLE ; 59-87 $
CRMODEL ; LHS = LNCP3 ; RHS = ONE,LNKWH,LNP13,LNP23 $
SAMPLE ; 88-116 $
CRMODEL ; LHS = LNCP3 ; RHS = ONE,LNKWH,LNP13,LNP23 $
SAMPLE ; 117-145 $
CRMODEL ; LHS = LNCP3 ; RHS = ONE,LNKWH,LNP13,LNP23 $
? Part (c)
SAMPLE ; 1-145 $
CREATE ; D1 = ORDER <= 129 $
create ; if(order >= 201 & order <= 229) D2=1 $
CREATE ; if(order >= 301 & order <= 329) D3=1 $
CREATE ; if(order >= 401 & order <= 429) D4=1 $
CREATE ; D5 = ORDER >= 501 $
CREATE ; LNKWH1 = LNKWH*D1
; LNKWH2 = LNKWH*D2
; LNKWH3 = LNKWH*D3
; LNKWH4 = LNKWH*D4
; LNKWH5 = LNKWH*D5 $
CRMODEL ; LHS=LNCP3 ; RHS = D1,D2,D3,D4,D5,LNKWH1,LNKWH2,LNKWH3,
LNKWH4,LNKWH5,LNP13,LNP23 $
? Part (f)
CREATE ; KWH2 = LNKWH*LNKWH $
CRMODEL ; LHS=LNCP3 ; RHS=ONE,LNKWH,KWH2,LNP13,LNP23 $
LIST ; ORDER,Lnkwh $_
*-* LIMDEP *-* File created 09/02/93 / 05:13:37
Notice that in order to estimate a separate set of coefficients for each size class we
just use a set of dummy variables defined over the observation index. The output from this
program is
Sample set to -> 1-29 MODEL COMMAND: CRMODEL;LHS=LNCP3;RHS=ONE,LNKWH,LNP13,LNP23$ Ordinary least squares regression. Dep. Variable = LNCP3 Observations = 29 Weights = ONE Mean of LHS = -0.3713174E+01 Std.Dev of LHS = 0.8075507E+00 StdDev of residuals= 0.5961617E+00 Sum of squares = 0.8885220E+01 R-squared = 0.5134018E+00 Adjusted R-squared= 0.4550100E+00 F[ 3, 25] = 0.8792363E+01 Log-likelihood = -0.2399707E+02 Restr.(á=0) Log-l = -0.3444166E+02 Amemiya Pr. Criter.= 0.1930833E+01 Akaike Info.Crit. = 0.4044307E+00 ANOVA Source Variation Degrees of Freedom Mean Square Regression 0.9374649E+01 3. 0.3124883E+01 Residual 0.8885220E+01 25. 0.3554088E+00 Total 0.1825987E+02 28. 0.6521382E+00 Durbin-Watson stat.= 1.7031035 Autocorrelation = 0.1484483 Variable Coefficient Std. Error t-ratio Prob|t|>x Mean of X Std.Dev.of X ------------------------------------------------------------------------------- Constant -3.3433 3.146 -1.063 0.29801 LNKWH 0.40029 0.8445E-01 4.740 0.00007 3.5015 1.3526 LNP13 0.61517 0.7293 0.843 0.40696 -2.6295 0.35401 LNP23 -0.81356E-01 0.7064 -0.115 0.90923 1.8908 0.36725 Sample set to -> 30-58 MODEL COMMAND: CRMODEL;LHS=LNCP3;RHS=ONE,LNKWH,LNP13,LNP23$ Ordinary least squares regression. Dep. Variable = LNCP3 Observations = 29 Weights = ONE Mean of LHS = -0.2149437E+01 Std.Dev of LHS = 0.3780031E+00 StdDev of residuals= 0.2424091E+00 Sum of squares = 0.1469054E+01 R-squared = 0.6328116E+00 Adjusted R-squared= 0.5887490E+00 F[ 3, 25] = 0.1436165E+02 Log-likelihood = 0.2099601E+01 Restr.(á=0) Log-l = -0.1242766E+02 Amemiya Pr. Criter.= 0.1310620E+00 Akaike Info.Crit. = 0.6686728E-01 ANOVA Source Variation Degrees of Freedom Mean Square Regression 0.2531764E+01 3. 0.8439214E+00 Residual 0.1469054E+01 25. 0.5876216E-01 Total 0.4000818E+01 28. 0.1428864E+00 Durbin-Watson stat.= 1.8593375 Autocorrelation = 0.0703312 Variable Coefficient Std. Error t-ratio Prob|t|òx Mean of X Std.Dev.of X ------------------------------------------------------------------------------- Constant -6.4890 1.413 -4.593 0.00011 LNKWH 0.65815 0.1163 5.659 0.00001 5.8950 0.39491 LNP13 0.93800E-01 0.2743 0.342 0.73523 -2.6112 0.32533 LNP23 0.37794 0.2765 1.367 0.18388 1.8645 0.32247 Sample set to -> 59-87 MODEL COMMAND: CRMODEL;LHS=LNCP3;RHS=ONE,LNKWH,LNP13,LNP23$ Ordinary least squares regression. Dep. Variable = LNCP3 Observations = 29 Weights = ONE Mean of LHS = -0.1406563E+01 Std.Dev of LHS = 0.2863842E+00 StdDev of residuals= 0.1980064E+00 Sum of squares = 0.9801633E+00 R-squared = 0.5731824E+00 Adjusted R-squared= 0.5219642E+00 F[ 3, 25] = 0.1119101E+02 Log-likelihood = 0.7967096E+01 Restr.(á=0) Log-l = -0.4378182E+01 Amemiya Pr. Criter.= -0.2735928E+00 Akaike Info.Crit. = 0.4461433E-01 ANOVA Source Variation Degrees of Freedom Mean Square Regression 0.1316282E+01 3. 0.4387606E+00 Residual 0.9801633E+00 25. 0.3920653E-01 Total 0.2296445E+01 28. 0.8201589E-01 Durbin-Watson stat.= 1.9969248 Autocorrelation = 0.0015376 Variable Coefficient Std. Error t-ratio Prob|t|<x Mean of X Std.Dev.of X ------------------------------------------------------------------------------- Constant -7.3329 1.689 -4.342 0.00021 LNKWH 0.93828 0.1980 4.740 0.00007 6.9605 0.19700 LNP13 0.40226 0.1994 2.017 0.05456 -2.6442 0.25783 LNP23 0.25001 0.1870 1.337 0.19334 1.8367 0.28288 Sample set to -> 88-116 MODEL COMMAND: CRMODEL;LHS=LNCP3;RHS=ONE,LNKWH,LNP13,LNP23$ Ordinary least squares regression. Dep. Variable = LNCP3 Observations = 29 Weights = ONE Mean of LHS = -0.4833377E+00 Std.Dev of LHS = 0.3192165E+00 StdDev of residuals= 0.1205973E+00 Sum of squares = 0.3635928E+00 R-squared = 0.8725656E+00 Adjusted R-squared= 0.8572735E+00 F[ 3, 25] = 0.5705979E+02 Log-likelihood = 0.2234652E+02 Restr.(á=0) Log-l = -0.7525705E+01 Amemiya Pr. Criter.= -0.1265277E+01 Akaike Info.Crit. = 0.1654974E-01 ANOVA Source Variation Degrees of Freedom Mean Square Regression 0.2489583E+01 3. 0.8298611E+00 Residual 0.3635928E+00 25. 0.1454371E-01 Total 0.2853176E+01 28. 0.1018992E+00 Durbin-Watson stat.= 2.0286206 Autocorrelation = -0.0143103 Variable Coefficient Std. Error t-ratio Prob|t|>x Mean of X Std.Dev.of X ------------------------------------------------------------------------------- Constant -6.5460 1.165 -5.620 0.00001 LNKWH 0.91204 0.1075 8.485 0.00000 7.6855 0.21247 LNP13 0.50696 0.1875 2.704 0.01215 -2.2746 0.38257 LNP23 0.93352E-01 0.1641 0.569 0.57453 2.2106 0.43737 Sample set to -> 117-145 MODEL COMMAND: CRMODEL;LHS=LNCP3;RHS=ONE,LNKWH,LNP13,LNP23$ Ordinary least squares regression. Dep. Variable = LNCP3 Observations = 29 Weights = ONE Mean of LHS = 0.3315352E+00 Std.Dev of LHS = 0.5052502E+00 StdDev of residuals= 0.1502536E+00 Sum of squares = 0.5644039E+00 R-squared = 0.9210378E+00 Adjusted R-squared= 0.9115624E+00 F[ 3, 25] = 0.9720246E+02 Log-likelihood = 0.1597036E+02 Restr.(á=0) Log-l = -0.2084205E+02 Amemiya Pr. Criter.= -0.8255418E+00 Akaike Info.Crit. = 0.2569011E-01 ANOVA Source Variation Degrees of Freedom Mean Square Regression 0.6583374E+01 3. 0.2194458E+01 Residual 0.5644039E+00 25. 0.2257616E-01 Total 0.7147778E+01 28. 0.2552778E+00 Durbin-Watson stat.= 1.9237334 Autocorrelation = 0.0381333 Variable Coefficient Std. Error t-ratio Prob|t|òx Mean of X Std.Dev.of X ------------------------------------------------------------------------------- Constant -6.7143 1.046 -6.417 0.00000 LNKWH 1.0444 0.6498E-01 16.072 0.00000 8.7408 0.44372 LNP13 0.60259 0.1973 3.054 0.00530 -2.5264 0.21829 LNP23 -0.28944 0.1749 -1.655 0.11039 1.9370 0.24615 Sample set to -> 1-145 MODEL COMMAND: CRMODEL;LHS=LNCP3;RHS=D1,D2,D3,D4,D5,LNKWH1,LNKWH2,LNKWH3,LN KWH4,LNKWH5,LNP13,LNP23$ Ordinary least squares regression. Dep. Variable = LNCP3 Observations = 145 Weights = ONE Mean of LHS = -0.1484195E+01 Std.Dev of LHS = 0.1482087E+01 StdDev of residuals= 0.3075163E+00 Sum of squares = 0.1257731E+02 R-squared = 0.9602371E+00 Adjusted R-squared= 0.9569485E+00 F[ 11, 133] = 0.2919843E+03 Log-likelihood = -0.2849526E+02 Restr.(á=0) Log-l = -0.2622948E+03 Amemiya Pr. Criter.= 0.5585553E+00 Akaike Info.Crit. = 0.1023924E+00 ANOVA Source Variation Degrees of Freedom Mean Square Regression 0.3037306E+03 11. 0.2761187E+02 Residual 0.1257731E+02 133. 0.9456627E-01 Total 0.3163079E+03 144. 0.2196583E+01 Durbin-Watson stat.= 1.7426507 Autocorrelation = 0.1286746 Variable Coefficient Std. Error t-ratio Prob|t|òx Mean of X Std.Dev.of X ------------------------------------------------------------------------------- D1 -4.1798 0.7022 -5.952 0.00000 0.20000 0.40139 D2 -5.0524 1.125 -4.491 0.00002 0.20000 0.40139 D3 -6.6301 2.237 -2.963 0.00361 0.20000 0.40139 D4 -6.7286 2.225 -3.024 0.00299 0.20000 0.40139 D5 -8.0834 1.380 -5.857 0.00000 0.20000 0.40139 LNKWH1 0.39688 0.4307E-01 9.214 0.00000 0.70030 1.5268 LNKWH2 0.64816 0.1472 4.402 0.00002 1.1790 2.3726 LNKWH3 0.88478 0.2973 2.976 0.00347 1.3921 2.7952 LNKWH4 0.90874 0.2737 3.321 0.00116 1.5371 3.0863 LNKWH5 1.0627 0.1313 8.091 0.00000 1.7482 3.5139 LNP13 0.42561 0.1632 2.608 0.01014 -2.5372 0.33858 LNP23 0.10373 0.1522 0.681 0.49675 1.9479 0.35980 MODEL COMMAND: CRMODEL;LHS=LNCP3;RHS=ONE,LNKWH,KWH2,LNP13,LNP23$ Ordinary least squares regression. Dep. Variable = LNCP3 Observations = 145 Weights = ONE Mean of LHS = -0.1484195E+01 Std.Dev of LHS = 0.1482087E+01 StdDev of residuals= 0.3076119E+00 Sum of squares = 0.1324751E+02 R-squared = 0.9581183E+00 Adjusted R-squared= 0.9569217E+00 F[ 4, 140] = 0.8006872E+03 Log-likelihood = -0.3225910E+02 Restr.(á=0) Log-l = -0.2622948E+03 Amemiya Pr. Criter.= 0.5139186E+00 Akaike Info.Crit. = 0.9788802E-01 ANOVA Source Variation Degrees of Freedom Mean Square Regression 0.3030604E+03 4. 0.7576510E+02 Residual 0.1324751E+02 140. 0.9462508E-01 Total 0.3163079E+03 144. 0.2196583E+01 Durbin-Watson stat.= 1.6652595 Autocorrelation = 0.1673702 Variable Coefficient Std. Error t-ratio Prob|t|>x Mean of X Std.Dev.of X ------------------------------------------------------------------------------- Constant -3.7646 0.7017 -5.365 0.00000 LNKWH 0.15255 0.6186E-01 2.466 0.01487 6.5567 1.9128 KWH2 0.50514E-01 0.5364E-02 9.418 0.00000 46.623 22.104 LNP13 0.48059 0.1611 2.984 0.00336 -2.5372 0.33858 LNP23 0.74166E-01 0.1500 0.494 0.62181 1.9479 0.35980
We are now prepared to test some hypotheses. Remember that the generic F-statistic is
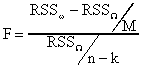
The trick is identifying or producing the requisite sums of squares. Sometimes it is easier to use
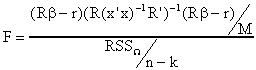
We'll first compute a few sums of squares. The residual sum of squares when it is assumed that the firms are from a single homogeneous population is RSS1=21.6403. When the equality restrictions on the intercepts and output coefficients are relaxed the the residual sum of squares is RSS2=12.5773. If intercepts, output coefficients and input price coefficients are allowed to be different across all five size classes then the residual sum of squares is RSS3=(.5644+.3636+.7802+1.4690+8.8852)=12.0624.
To test the hypothesis that the respective coefficients are equal across all size classes against the alternative that each class has a different set of coefficients one computes F=((21.6403-12.0624)/16)/(12.0624/(145-20))=6.2. The critical F at the 5% level is about 1.7, so we reject the null of equal coefficients.
Next, test the null hypothesis that the respective coefficients are equal across all size classes against the alternative that the price coefficients are equal but the intercepts and output coefficients are not. The observed statistic is F=((21.6403-12.5773)/8)/(12.5773/(145-12))=11.98, so we reject the null.
Next, test the null that the respective price coefficients are equal against the alternate that the coefficients are unique across size classes. Under both hypotheses the intercepts and output coefficients are allowed to differ. The observed statistic is F=(( 12.5773-12.0624)/8)/(12.0624/(145-20))=.66. We cannot reject the null. The preferred model is one in which the price coefficients are constrained to be equal, but the output coefficients and intercepts are not equal across size class.
In order to test the last hypothesis that the intercepts and price coefficients are
equal across size class but returns to scale differs by firm size we will use the second
construction of the F-test shown above to test the joint restriction that the coefficient
on the output variable is one and the coefficient on the output squared term is zero.
This is an extremely large F so we reject the null that returns to scale are constant. Indeed, just looking at the t-statistics in the last set of results should have been enough to know that the coefficient Since the F is constructed in MathView you can change the values on the output and output-squared terms in b ( the second and third elements ) to see just how different things would have to have been in order to accept the null.