3.6 An Example of REM and LSDV
In this rather lengthy example to show the relationships between the REM and LSDV
model we explore several different transformations of the data and model specifications.
In a set of examples we will use all fifty observations. In two sets of results we will
use the five observations on the individual means and the ten observations on the time
means.
The following tables show the means of the variables in column two. The other columns are
standard deviation, minimum and maximum. The original data is from problem set 2.
Group means for the independent variable.
1 2 3 4 5
ROW 1 10.0000 30.6060 11.5886 41.6700 3.78000
ROW 2 10.0000 29.7270 8.92409 47.7000 18.6600
ROW 3 10.0000 25.9480 8.81008 41.4200 12.5600
ROW 4 10.0000 28.4260 9.72321 42.2500 14.8000
ROW 5 10.0000 24.3030 12.4954 41.4400 5.75000
Group means for the dependent variable
1 2 3 4 5
ROW 1 10.0000 47.8690 12.9291 65.2700 21.7100
ROW 2 10.0000 37.2290 9.54634 49.3900 16.2100
ROW 3 10.0000 38.1330 10.5279 51.3700 14.5100
ROW 4 10.0000 40.7300 14.6780 56.1200 9.31000
ROW 5 10.0000 34.5160 12.4180 47.9600 14.8300
Time means for the independent variable
1 2 3 4 5
ROW 1 5.00000 36.9220 4.07979 41.8600 32.5200
ROW 2 5.00000 25.5600 7.09338 35.3200 18.5200
ROW 3 5.00000 22.2480 11.2742 34.2100 3.78000
ROW 4 5.00000 21.7460 8.68052 35.3400 14.0200
ROW 5 5.00000 28.0860 5.30027 35.1300 20.8300
ROW 6 5.00000 27.3200 11.5646 39.1900 10.3700
ROW 7 5.00000 25.3820 18.2429 47.7000 5.75000
ROW 8 5.00000 21.6140 7.45824 30.7100 12.5600
ROW 9 5.00000 30.7500 5.37027 36.8600 23.7000
ROW 10 5.00000 38.3920 6.26952 42.2500 27.3200
Time means for the dependent variable
1 2 3 4 5
ROW 1 5.00000 50.1320 6.60087 60.5900 42.7900
ROW 2 5.00000 41.3000 6.60381 50.0400 33.8200
ROW 3 5.00000 20.4060 11.9642 40.2900 9.31000
ROW 4 5.00000 39.4320 8.72853 49.9100 25.6100
ROW 5 5.00000 34.6540 7.38297 45.8800 28.2400
ROW 6 5.00000 42.3960 13.0091 53.5500 20.7900
ROW 7 5.00000 45.6340 18.8894 65.2700 14.8300
ROW 8 5.00000 35.2340 10.1048 45.0000 22.8000
ROW 9 5.00000 38.1080 5.73346 44.6200 31.8600
ROW 10 5.00000 49.6580 7.52705 59.1800 42.6200
Grand MEAN of the dependent variable Y = 39.6954
Grand mean of the independent variable X = 27.8020
The following table presents the results using OLS, before anything has been done to the
data.
Ordinary least squares regression. Dep. Variable = Y
Observations = 50 Weights = ONE
Mean of LHS = 0.3969540E+02 Std.Dev of LHS = 0.1252044E+02
StdDev of residuals= 0.1067064E+02 Sum of squares = 0.5465407E+04
Rsquared = 0.2884798E+00 Adjusted Rsquared= 0.2736564E+00
F[ 1, 48] = 0.1946119E+02
Loglikelihood = 0.1883012E+03 Restr.(ß=0) Logl = 0.1968100E+03
Amemiya Pr. Criter.= 0.7612048E+01 Akaike Info.Crit. = 0.1184171E+03
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.2215902E+04 1. 0.2215902E+04
Residual 0.5465407E+04 48. 0.1138626E+03
Total 0.7681309E+04 49. 0.1567614E+03
DurbinWatson stat.= 2.1803752 Autocorrelation = 0.0901876
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
Constant 21.470 4.398 4.881 0.00001
X1 0.65554 0.1486 4.411 0.00006 27.802 10.258
The following table presents the results for a model in which the data has been
transformed by subtracting off the appropriate group mean and the grand mean from each
data point.
Ordinary least squares regression. Dep. Variable = YIND
Observations = 50 Weights = ONE
Mean of LHS = 0.3969540E+02 Std.Dev of LHS = 0.1164879E+02
StdDev of residuals= 0.1002805E+02 Sum of squares = 0.4826970E+04
Rsquared = 0.2740333E+00 Adjusted Rsquared= 0.2589090E+00
F[ 1, 48] = 0.1811873E+02
Loglikelihood = 0.1851957E+03 Restr.(ß=0) Logl = 0.1932020E+03
Amemiya Pr. Criter.= 0.7487828E+01 Akaike Info.Crit. = 0.1045843E+03
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.1822054E+04 1. 0.1822054E+04
Residual 0.4826970E+04 48. 0.1005619E+03
Total 0.6649024E+04 49. 0.1356944E+03
DurbinWatson stat.= 2.4034218 Autocorrelation = 0.2017109
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
Constant 22.707 4.235 5.361 0.00000
XIND 0.61104 0.1436 4.257 0.00010 27.802 9.9796
In this table we present the results for the original data, but with the group dummies
included. As we found in the lecture notes, the slope coefficients are the same as those
in the ANOVA model.
Ordinary least squares regression. Dep. Variable = Y
Observations = 50 Weights = ONE
Mean of LHS = 0.3969540E+02 Std.Dev of LHS = 0.1252044E+02
StdDev of residuals= 0.1047396E+02 Sum of squares = 0.4826970E+04
Rsquared = 0.3715954E+00 Adjusted Rsquared= 0.3001858E+00
F[ 5, 44] = 0.5203717E+01
Loglikelihood = 0.1851957E+03 Restr.(ß=0) Logl = 0.1968100E+03
Amemiya Pr. Criter.= 0.7647828E+01 Akaike Info.Crit. = 0.1228683E+03
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.2854339E+04 5. 0.5708678E+03
Residual 0.4826970E+04 44. 0.1097039E+03
Total 0.7681309E+04 49. 0.1567614E+03
DurbinWatson stat.= 2.4034217 Autocorrelation = 0.2017109
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
X1 0.61104 0.1499 4.075 0.00019 27.802 10.258
I1 29.168 5.659 5.154 0.00001 0.20000 0.40406
I2 19.065 5.553 3.433 0.00131 0.20000 0.40406
I3 22.278 5.109 4.360 0.00008 0.20000 0.40406
I4 23.361 5.398 4.328 0.00009 0.20000 0.40406
I5 19.666 4.924 3.994 0.00024 0.20000 0.40406
A graphical view of the individual effects model provides
some insight into the gains from this approach.
In the following table we present the results for a regression in which the group mean
appears in each period and then grand means have been subtracted.
Ordinary least squares regression. Dep. Variable = YIND
Observations = 50 Weights = ONE
Mean of LHS = 0.7629395E06 Std.Dev of LHS = 0.4589886E+01
StdDev of residuals= 0.3057628E+01 Sum of squares = 0.4581054E+03
Rsquared = 0.5562222E+00 Adjusted Rsquared= 0.5562222E+00
F[ 1, 49] = 0.6141561E+02
Loglikelihood = 0.1263238E+03 Restr.(ß=0) Logl = 0.1466346E+03
Amemiya Pr. Criter.= 0.5092953E+01 Akaike Info.Crit. = 0.9536071E+01
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.5741801E+03 1. 0.5741801E+03
Residual 0.4581054E+03 49. 0.9349090E+01
Total 0.1032285E+04 49. 0.2106705E+02
DurbinWatson stat.= 0.2820563 Autocorrelation = 0.8589718
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
XIND 1.4414 0.1839 7.837 0.00000 0.38147E06 2.3749
The following table is based on the five observations we have remaining after we
average across time for each individual. Not surprisingly, the slope coefficient looks
just like the table above it. If you will look at section 3.3 Estimation in the
lecture notes, you will see that this equivalence was pointed out in step 1.a
Ordinary least squares regression. Dep. Variable = Y
Observations = 5 Weights = ONE
Mean of LHS = 0.3969540E+02 Std.Dev of LHS = 0.5080072E+01
StdDev of residuals= 0.3907707E+01 Sum of squares = 0.4581052E+02
Rsquared = 0.5562224E+00 Adjusted Rsquared= 0.4082965E+00
F[ 1, 3] = 0.3760143E+01
Loglikelihood = 0.1263238E+02 Restr.(ß=0) Logl = 0.1466346E+02
Amemiya Pr. Criter.= 0.5852953E+01 Akaike Info.Crit. = 0.2137824E+02
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.5741803E+02 1. 0.5741803E+02
Residual 0.4581052E+02 3. 0.1527017E+02
Total 0.1032285E+03 4. 0.2580714E+02
DurbinWatson stat.= 2.8205634 Autocorrelation = 0.4102817
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
Constant 0.37733 20.74 0.018 0.98663
X 1.4414 0.7433 1.939 0.14784 27.802 2.6286
In the table which follows, we have subtracted the appropriate time mean and grand
mean from each observation.
Ordinary least squares regression. Dep. Variable = YTIM
Observations = 50 Weights = ONE
Mean of LHS = 0.3969540E+02 Std.Dev of LHS = 0.9383881E+01
StdDev of residuals= 0.8391422E+01 Sum of squares = 0.3379966E+04
Rsquared = 0.2166583E+00 Adjusted Rsquared= 0.2003386E+00
F[ 1, 48] = 0.1327594E+02
Loglikelihood = 0.1762869E+03 Restr.(ß=0) Logl = 0.1823915E+03
Amemiya Pr. Criter.= 0.7131475E+01 Akaike Info.Crit. = 0.7323260E+02
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.9348379E+03 1. 0.9348379E+03
Residual 0.3379966E+04 48. 0.7041596E+02
Total 0.4314804E+04 49. 0.8805722E+02
DurbinWatson stat.= 1.9365728 Autocorrelation = 0.0317136
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
Constant 25.431 4.091 6.217 0.00000
XTIM 0.51307 0.1408 3.644 0.00066 27.802 8.5133
The following table presents the results for the model with time dummies used with the
original data. Once again we see that the ANOVA and LSDV models are the same.
Ordinary least squares regression. Dep. Variable = Y
Observations = 50 Weights = ONE
Mean of LHS = 0.3969540E+02 Std.Dev of LHS = 0.1252044E+02
StdDev of residuals= 0.9309447E+01 Sum of squares = 0.3379966E+04
Rsquared = 0.5599752E+00 Adjusted Rsquared= 0.4471484E+00
F[ 10, 39] = 0.4963137E+01
Loglikelihood = 0.1762869E+03 Restr.(ß=0) Logl = 0.1968100E+03
Amemiya Pr. Criter.= 0.7491475E+01 Akaike Info.Crit. = 0.1057323E+03
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.4301343E+04 10. 0.4301343E+03
Residual 0.3379966E+04 39. 0.8666580E+02
Total 0.7681309E+04 49. 0.1567614E+03
DurbinWatson stat.= 1.9365728 Autocorrelation = 0.0317136
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
X1 0.51307 0.1562 3.284 0.00216 27.802 10.258
T1 31.189 7.113 4.384 0.00009 0.10000 0.30305
T2 28.186 5.769 4.886 0.00002 0.10000 0.30305
T3 8.9913 5.423 1.658 0.10536 0.10000 0.30305
T4 28.275 5.373 5.262 0.00001 0.10000 0.30305
T5 20.244 6.048 3.347 0.00182 0.10000 0.30305
T6 28.379 5.962 4.760 0.00003 0.10000 0.30305
T7 32.611 5.749 5.672 0.00000 0.10000 0.30305
T8 24.145 5.360 4.504 0.00006 0.10000 0.30305
T9 22.331 6.357 3.513 0.00114 0.10000 0.30305
T10 29.960 7.301 4.104 0.00020 0.10000 0.30305
A graphical view of the time fixed effects model
clarifies the issues a bit.
In the following table, the time mean is used for each individual, then the grand mean
is subtracted.
Ordinary least squares regression. Dep. Variable = YTIM
Observations = 50 Weights = ONE
Mean of LHS = 0.1907349E06 Std.Dev of LHS = 0.8288798E+01
StdDev of residuals= 0.6150913E+01 Sum of squares = 0.1853853E+04
Rsquared = 0.4493242E+00 Adjusted Rsquared= 0.4493242E+00
F[ 1, 49] = 0.3998158E+02
Loglikelihood = 0.1612719E+03 Restr.(ß=0) Logl = 0.1761871E+03
Amemiya Pr. Criter.= 0.6490875E+01 Akaike Info.Crit. = 0.3859040E+02
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.1512652E+04 1. 0.1512652E+04
Residual 0.1853853E+04 49. 0.3783373E+02
Total 0.3366505E+04 49. 0.6870418E+02
DurbinWatson stat.= 2.7435652 Autocorrelation = 0.3717826
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
XTIM 0.97077 0.1535 6.323 0.00000 0.19073E06 5.7234
The table which follows is based on the ten observations which result when we average
across people. The slope coefficient differs a bit due to rounding errors.
Ordinary least squares regression. Dep. Variable = Y
Observations = 10 Weights = ONE
Mean of LHS = 0.3969460E+02 Std.Dev of LHS = 0.8650567E+01
StdDev of residuals= 0.6809286E+01 Sum of squares = 0.3709310E+03
Rsquared = 0.4492411E+00 Adjusted Rsquared= 0.3803962E+00
F[ 1, 8] = 0.6525412E+01
Loglikelihood = 0.3225654E+02 Restr.(ß=0) Logl = 0.3523883E+02
Amemiya Pr. Criter.= 0.6851308E+01 Akaike Info.Crit. = 0.5563965E+02
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.3025597E+03 1. 0.3025597E+03
Residual 0.3709310E+03 8. 0.4636638E+02
Total 0.6734907E+03 9. 0.7483230E+02
DurbinWatson stat.= 2.7358262 Autocorrelation = 0.3679131
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
Constant 12.704 10.78 1.178 0.27260
X 0.97082 0.3800 2.554 0.03394 27.802 5.9724
The following results occur when we subtract group and time means, then add back the
grand mean. This is the fully saturated ANOVA model.
Ordinary least squares regression. Dep. Variable = YIND
Observations = 50 Weights = ONE
Mean of LHS = 0.5531311E06 Std.Dev of LHS = 0.8184753E+01
StdDev of residuals= 0.7372867E+01 Sum of squares = 0.2663599E+04
Rsquared = 0.1885503E+00 Adjusted Rsquared= 0.1885503E+00
F[ 1, 49] = 0.1138575E+02
Loglikelihood = 0.1703322E+03 Restr.(ß=0) Logl = 0.1755555E+03
Amemiya Pr. Criter.= 0.6853288E+01 Akaike Info.Crit. = 0.5544634E+02
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.6189198E+03 1. 0.6189198E+03
Residual 0.2663599E+04 49. 0.5435916E+02
Total 0.3282519E+04 49. 0.6699018E+02
DurbinWatson stat.= 2.3226517 Autocorrelation = 0.1613258
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
XIND 0.43473 0.1288 3.374 0.00145 0.41962E06 8.1753
When we include both time and group dummies with the original data we get the
following results. Of course, slope coefficient results are the same as the ANOVA model in
the the table above.
Ordinary least squares regression. Dep. Variable = Y
Observations = 50 Weights = ONE
Mean of LHS = 0.3969540E+02 Std.Dev of LHS = 0.1252044E+02
StdDev of residuals= 0.8723693E+01 Sum of squares = 0.2663599E+04
Rsquared = 0.6532363E+00 Adjusted Rsquared= 0.5145308E+00
F[ 14, 35] = 0.4709521E+01
Loglikelihood = 0.1703322E+03 Restr.(ß=0) Logl = 0.1968100E+03
Amemiya Pr. Criter.= 0.7413288E+01 Akaike Info.Crit. = 0.9893367E+02
ANOVA Source Variation Degrees of Freedom Mean Square
Regression 0.5017710E+04 14. 0.3584078E+03
Residual 0.2663599E+04 35. 0.7610283E+02
Total 0.7681309E+04 49. 0.1567614E+03
DurbinWatson stat.= 2.3226517 Autocorrelation = 0.1613258
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
X1 0.43473 0.1524 2.852 0.00725 27.802 10.258
I1 39.923 7.794 5.122 0.00001 0.20000 0.40406
I2 29.665 7.686 3.859 0.00047 0.20000 0.40406
I3 32.212 7.234 4.453 0.00008 0.20000 0.40406
I4 33.731 7.529 4.480 0.00008 0.20000 0.40406
I5 29.310 7.043 4.162 0.00020 0.20000 0.40406
T1 1.1130 5.522 0.202 0.84142 0.10000 0.30305
T2 2.7796 5.854 0.475 0.63786 0.10000 0.30305
T3 22.234 6.041 3.680 0.00078 0.10000 0.30305
T4 2.9895 6.073 0.492 0.62560 0.10000 0.30305
T5 10.524 5.737 1.834 0.07510 0.10000 0.30305
T6 2.4487 5.770 0.424 0.67387 0.10000 0.30305
T7 1.6318 5.863 0.278 0.78240 0.10000 0.30305
T8 7.1302 6.081 1.172 0.24893 0.10000 0.30305
T9 8.2278 5.639 1.459 0.15346 0.10000 0.30305
In the preceding two cases the efficiency of the estimator is greatly reduced by the
large number of coefficients to be estimated.
In the tables which follow we will be exploring the choice of model specification. One
alternative is a model with no regressors. The possibility that arises is that the group
means are no different from the grand mean. The model has only an intercept. We might term
this simplest case model one. An alternative is to compare group means of the dependent
variable with the grand mean. We might term such a specification model two. A third
possibility is that the correct model is one with only regressors; model three. The final
possibility has both group dummies and regressors; model four.
Panel Data Analysis of Y [One way]
Means of variables:
LHS RHS
Group Size Y X1
0 50 0.3970E+02 0.2780E+02
1 10 0.4787E+02 0.3061E+02
2 10 0.3723E+02 0.2973E+02
3 10 0.3813E+02 0.2595E+02
4 10 0.4073E+02 0.2843E+02
5 10 0.3452E+02 0.2430E+02
Unconditional ANOVA (No regressors)
Source Variation Deg. Free. Mean Square
Between 1032.28 4. 258.071
Residual 6649.02 45. 147.756
Total 7681.31 49. 156.761
Test Statistics for the Classical Model
Model LogLikelihood Sum of Squares Rsquared
(1) Constant term only 196.80998 0.768131E+04 0.0000000
(2) Group effects only 193.20198 0.664902E+04 0.1343892
(3) X variables only 188.30120 0.546541E+04 0.2884798
(4) X and group effects 185.19571 0.482697E+04 0.3715954
Hypothesis Tests
Likelihood Ratio Test F Tests
Chisquared d.f. Prob value F num. denom. Prob value
(2) vs (1) 7.216 4 0.12490 1.747 4 44 0.15689
(3) vs (1) 17.018 1 0.00004 19.461 1 48 0.00006
(4) vs (1) 23.229 5 0.00031 5.204 5 44 0.00077
(4) vs (2) 16.013 1 0.00006 16.609 1 44 0.00019
(4) vs (3) 6.211 4 0.18394 1.455 4 44 0.23217
Another alternative is that the differences between groups are not fixed, but are
random. The explanatory variables in the model are an intercept and the regressors. The
error covariance is not scalar diagonal.
Random Effects Model: v(i,t) = e(i,t) + u(i)
2 estimates of Var[u] + Q * Var[e]
Based on Means OLS
0.15270E+02 0.20959E+02
(Used Means. Q = 0.1000)
Estimates: Var[e] = 0.109704E+03
Var[u] = 0.429980E+01
Corr[v(i,t),v(i,s)] = 0.037716
To choose between the Random Effects Model and OLS we use the LM test.
The null is that the variance component for randomness across groups is zero.
Lagrange Multiplier Test vs. Model (3) = 0.06288
( 1 df, prob value = 0.801999)
Since the test statistic is quite small we do not reject OLS in favor of REM.
In choosing between the REM and the LSDV model the null is specified such that the two
sets of coefficients are equal, though the REM is more efficient. Under the alternate
hypothesis the regressor might be correlated with the error term in the REM due to
ommitted variables.
Fixed vs. Random Effects (Hausman) = 1.19903
( 1 df, prob value = 0.273515)
Since the test statistic is quite small we do not reject the null,
that LSDV and REM are essentially the same.
On the basis of the Hausman test we would choose the REM, but we have already
seen that under the LM test we prefer the OLS model over REM.
The regression results for the REM with group effects follow. This is a feasible GLS estimator.
Estd. Autocorrelation of e(i,t) 0.233766
Reestimated using GLS coefficients:
Estimates: Var[e] = 0.109821E+03
Var[u] = 0.101526E+02
Sum of Squares 0.546615E+04
Rsquared 0.288382E+00
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
X1 0.64350 0.1470 4.378 0.00001 27.802 10.258
Constant 21.805 4.444 4.906 0.00000
Since we have panel data, it might be the case that there are systematic differences
across periods rather than groups/persons. The tabulated results follow the same scheme as
those we just looked at for group differences. Initially we consider the question of
whether or not there is a model which has just a grand mean, then we look at time means,
then a model with time dummies and regressors. Since the OLS and time dummy models are
presented above, we do not repeat them here.
Panel Data Analysis of Y [One way]
Means of variables:
LHS RHS
Group Size Y X1
0 50 0.3970E+02 0.2780E+02
1 5 0.5013E+02 0.3692E+02
2 5 0.4130E+02 0.2556E+02
3 5 0.2041E+02 0.2225E+02
4 5 0.3943E+02 0.2175E+02
5 5 0.3465E+02 0.2809E+02
6 5 0.4240E+02 0.2732E+02
7 5 0.4563E+02 0.2538E+02
8 5 0.3523E+02 0.2161E+02
9 5 0.3811E+02 0.3075E+02
10 5 0.4966E+02 0.3839E+02
Unconditional ANOVA (No regressors)
Source Variation Deg. Free. Mean Square
Between 3366.50 9. 374.056
Residual 4314.80 40. 107.870
Total 7681.31 49. 156.761
Test Statistics for the Classical Model
(Note that I have changed the labels in the tables to reflect the fact that we
are thinking about effects in the time domain.)
Model LogLikelihood Sum of Squares Rsquared
(1) Constant term only 196.80998 0.768131E+04 0.0000000
(2) Time effects only 182.39153 0.431480E+04 0.4382723
(3) X variables only 188.30120 0.546541E+04 0.2884798
(4) X and time effects 176.28688 0.337997E+04 0.5599752
Hypothesis Tests
Likelihood Ratio Test F Tests
Chisquared d.f. Prob value F num. denom. Prob value
(2) vs (1) 28.837 9 0.00069 3.468 9 39 0.00315
(3) vs (1) 17.018 1 0.00004 19.461 1 48 0.00006
(4) vs (1) 41.046 10 0.00001 4.963 10 39 0.00012
(4) vs (2) 12.209 1 0.00048 10.787 1 39 0.00216
(4) vs (3) 24.029 9 0.00426 2.674 9 39 0.01603
Once again we must also consider the possibility that there is a random shock specific
to each period but common to all persons/groups. This calls for another REM estimation
with a time effect.
Random Effects Model: v(i,t) = e(i,t) + u(t)
2 estimates of Var[u] + Q * Var[e]
Based on Means OLS
0.46346E+02 0.50334E+02
(Used Means. Q = 0.2000)
Estimates: Var[e] = 0.866658E+02
Var[u] = 0.290132E+02
Corr[v(i,t),v(i,s)] = 0.250808
OLS vs. REM
Lagrange Multiplier Test vs. Model (3) = 4.43002
( 1 df, prob value = 0.035312)
This time the test statistic is rather large,
so we reject the OLS model in favor of the REM specification.
Fixed vs. Random Effects (Hausman) = 1.24126
( 1 df, prob value = 0.265228)
Since we observe a small test statistic we do not reject the null. Under the null the
LSDV and REM produce the same result. However the REM is more efficient so we choose that
model. The feasible GLS estimates for the REM follow:
Estd. Autocorrelation of e(i,t) 0.000000
Reestimated using GLS coefficients:
Estimates: Var[e] = 0.870646E+02
Var[u] = 0.350846E+02
Sum of Squares 0.549542E+04
Rsquared 0.284572E+00
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
X1 0.57925 0.1445 4.009 0.00006 27.802 10.258
Constant 23.591 4.557 5.176 0.00000
As a last possibility we might consider effects in both the time and group domain.
This is often referred to in the statistics literature as a two way analysis of variance.
In the table of hypothesis tests there are some rows repeated from the earlier tables. The
new rows are those involving model five. You will note that these are not produced by
LIMDEP when you call for both time and person effects in the REM model.
Panel Data Analysis of Y [Two way]
Test Statistics for the Classical Model
Model LogLikelihood Sum of Squares Rsquared
(1) Constant term only 196.80998 0.768131E+04 0.0000000
(2a) Group effects only 193.20198 0.664902E+04 0.1343892
(2b) Time effects only -182.39153 0.431480E+04 0.4382723
(3) X variables only 188.30120 0.546541E+04 0.2883824
(4a) X and group effects 185.19571 0.482697E+04 0.3715954
(4b) X and time effects 176.28688 0.337997E+04 0.5599752
(5) X ind.&time effects 170.33219 0.266360E+04 0.6532363
Hypothesis Tests
Likelihood Ratio Test F Tests
Chisquared d.f. Prob value F num. denom. Prob value
(2a) vs (1) 7.216 4 0.12490 1.747 4 44 0.15689
(2b) vs (1) 28.837 9 0.00069 3.468 9 39 0.00315
(3) vs (1) 17.018 1 0.00004 19.461 1 48 0.00006
(4a) vs (1) 23.229 5 0.00031 5.204 5 44 0.00077
(4b) vs (1) 41.046 10 0.00001 4.963 10 39 0.00012
(4a) vs (2a) 16.013 1 0.00006 16.609 1 44 0.00019
(4b) vs (2b) 12.209 1 0.00048 10.787 1 39 0.00216
(4a) vs (3) 6.211 4 0.18394 1.455 4 44 0.23217
(4b) vs (3) 24.029 9 0.00426 2.674 9 39 0.01603
(5) vs (1) 52.955 15 0.00000 4.269 14 35 0.00024
(5) vs (3) 35.938 13 0.00061 2.554 13 35 0.01366
(5) vs (4a) 29.727 9 0.00048 3.158 9 35 0.00682
(5) vs (4b) 11.909 4 0.01804 2.353 4 35 0.07292
In looking through the hypothesis tests we see that the only time we fail to reject
the zero restrictions on the dummy variables is in the comparison between models (4a) and
(3). The group dummies don't seem to add much to the model with just the independent
variable.
Estimates: Var[e] = 0.761028E+02
Var[u] = 0.765991E+01
Corr[v(i,t),v(i,s)] = 0.091448
Var[w] = 0.311257E+02
Corr[v(i,t),v(j,t)] = 0.290275
First we test the REM specification against OLS. The chi-square is significant
at the 10% level so we might be inclined to reject OLS in favor of the random
effects model.
Lagrange Multiplier Test vs. Model (3) = 4.49290
( 2 df, prob value = 0.105774)
Fixed vs. Random Effects (Hausman) = 2.91479
( 1 df, prob value = 0.087771)
Using the Hausman test we are inclined to reject the REM specification in favor of the
LSDV model. Among the LSDV models, the table of hypothesis tests suggests that we go with
the fully saturated model.
Estd. Autocorrelation of e(i,t) 0.151310
Reestimated using GLS coefficients:
Estimates: Var[e] = 0.771724E+02
Var[u] = 0.150105E+02
Var[w] = 0.421922E+02
Sum of Squares 0.553230E+04
Rsquared 0.279771E+00
Variable Coefficient Std. Error tratio Prob|t|³x Mean of X Std.Dev.of X
�
73;
X1 0.54164 0.1390 3.897 0.00010 27.802 10.258
Constant 24.637 4.593 5.364 0.00000
The table that follows is the set of OLS residuals, their sums by group and time,
squares of the sums, and sum of the squared group and time sums. You could use these to
calculate the LM statistics reported above in the tests for discriminating between REM and
OLS.
Residuals from the OLS regression using no dummies and
all of the data.
Person
Time 1 2 3 4 5 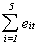
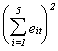 1 13.9078 0.0017 8.3588 0.9610 0.9828 22.2902 496.8539
2 5.4162 0.0847 9.2193 4.0984 3.4472 15.3716 236.2871
3 2.2379 22.9662 21.9916 34.5861 3.5393 78.2425 6121.896
4 5.2731 6.7375 2.4383 9.1345 5.0507 18.5328 343.4657
5 3.2350 8.4987 16.2592 9.8896 5.2747 26.1378 683.1872
6 5.6584 5.7907 5.7102 16.9828 7.4779 15.0828 227.4911
7 16.4835 3.3493 11.6723 23.2280 10.4094 37.6250 1415.641
8 3.3982 4.8737 8.0163 8.9838 9.3291 2.0245 4.0986
9 0.4236 11.6166 5.6723 0.2788 1.0133 17.5997 309.7504
10 11.7964 3.2405 4.9625 6.9533 1.9256 15.1020 228.0710 10066.74
1 13.9078 0.0017 8.3588 0.9610 0.9828 22.2902 496.8539
2 5.4162 0.0847 9.2193 4.0984 3.4472 15.3716 236.2871
3 2.2379 22.9662 21.9916 34.5861 3.5393 78.2425 6121.896
4 5.2731 6.7375 2.4383 9.1345 5.0507 18.5328 343.4657
5 3.2350 8.4987 16.2592 9.8896 5.2747 26.1378 683.1872
6 5.6584 5.7907 5.7102 16.9828 7.4779 15.0828 227.4911
7 16.4835 3.3493 11.6723 23.2280 10.4094 37.6250 1415.641
8 3.3982 4.8737 8.0163 8.9838 9.3291 2.0245 4.0986
9 0.4236 11.6166 5.6723 0.2788 1.0133 17.5997 309.7504
10 11.7964 3.2405 4.9625 6.9533 1.9256 15.1020 228.0710 10066.74
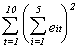
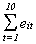 63.3545 37.2832 3.47025 6.2554 28.8565
63.3545 37.2832 3.47025 6.2554 28.8565
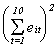 4013.795 1390.038 12.04263 39.13009 832.7027
4013.795 1390.038 12.04263 39.13009 832.7027
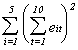 6287.709
6287.709
The three Random Effects Models are pictured graphically.
All of the statistical tests and choice of model can be analyzed with some summary tables.
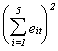 1 13.9078 0.0017 8.3588 0.9610 0.9828 22.2902 496.8539
2 5.4162 0.0847 9.2193 4.0984 3.4472 15.3716 236.2871
3 2.2379 22.9662 21.9916 34.5861 3.5393 78.2425 6121.896
4 5.2731 6.7375 2.4383 9.1345 5.0507 18.5328 343.4657
5 3.2350 8.4987 16.2592 9.8896 5.2747 26.1378 683.1872
6 5.6584 5.7907 5.7102 16.9828 7.4779 15.0828 227.4911
7 16.4835 3.3493 11.6723 23.2280 10.4094 37.6250 1415.641
8 3.3982 4.8737 8.0163 8.9838 9.3291 2.0245 4.0986
9 0.4236 11.6166 5.6723 0.2788 1.0133 17.5997 309.7504
10 11.7964 3.2405 4.9625 6.9533 1.9256 15.1020 228.0710 10066.74
1 13.9078 0.0017 8.3588 0.9610 0.9828 22.2902 496.8539
2 5.4162 0.0847 9.2193 4.0984 3.4472 15.3716 236.2871
3 2.2379 22.9662 21.9916 34.5861 3.5393 78.2425 6121.896
4 5.2731 6.7375 2.4383 9.1345 5.0507 18.5328 343.4657
5 3.2350 8.4987 16.2592 9.8896 5.2747 26.1378 683.1872
6 5.6584 5.7907 5.7102 16.9828 7.4779 15.0828 227.4911
7 16.4835 3.3493 11.6723 23.2280 10.4094 37.6250 1415.641
8 3.3982 4.8737 8.0163 8.9838 9.3291 2.0245 4.0986
9 0.4236 11.6166 5.6723 0.2788 1.0133 17.5997 309.7504
10 11.7964 3.2405 4.9625 6.9533 1.9256 15.1020 228.0710 10066.74
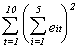
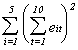 6287.709
6287.709