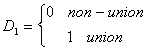
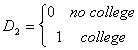
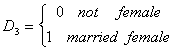
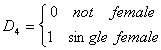
SPECIFICATION PROBLEMS: Part 3

Dummy Variables and Splines

The models discussed in this section are variants of the ANOVA models discussed earlier.  You will see that they are very closely related to the earlier work on restrictions and tests of hypothesis.

Dummy Variables
Case 1
Suppose we have earnings data on workers who can be divided as

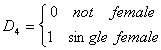
We also have a continuous variable called x, perhaps age, so the full model is

Using OLS to estimate all the parameters we can then discuss the effects of membership in particular groups. For example, suppose that we want to predict the earnings of a non-union, uneducated male. The predicted earnings, conditional on x, are

If we have a union member, educated, single female then the predicted earnings are

The idea is that each group has its own independent intercept, but all have the same slope on x.

Case 2

We could use dummies to model different slopes for different groups. Consider an example with just two groups.

We have the model with one RHS variable

If the individual is a male then we get

For a female

The female differs from the male in both intercept and slope. In this case, in which all of the RHS variables receive the dummy variable treatment, we could apply OLS to the individual subsets of data and get the same results. In an instance where some slope is common then we want to apply OLS to the pooled data.

Case 3

Suppose we have a quarterly time series. Instead of setting up a dummy variable for three of the four quarters as in

we get lazy and construct a variable that takes the following form

Then, blundering along, we estimate the three parameters of

The results by quarter are

First Quarter: 

Second Quarter: 

Third Quarter: 

Fourth Quarter: 

The effect of creating this funny RHS variable, S, to account for the seasonal differences is to make the quarter-to-quarter shift the same between any pair of quarters. Is this plausible? You will also see this kind of careless construction in cross sections in which firms in industry 1 have a variable with a value of 1, firms in industry 2 have a variable with a value of 2 and so on.

2. Splines

Splines have their origin in architecture and engineering. In those disciplines a fair curve needs to be fitted to a set of points and a french curve just won't do the trick. Instead they use a flexible rubber edge which can be bent to any curve. It is held in place by weights called ducks. A point where the curve changes its shape is called a knot.
Return to the earlier example in which there were two groups of wage earners differing in slope and intercept, but the slope did not change as the worker aged. The estimated model would appear


But suppose, in a new study, we think that the rate of change of wages should depend on age. The model needs to be modified so that the slope coefficient differs over prespecified intervals. There is also the stipulation that the resulting curve be continuous at the points where there is a change in slope. The new model should look like

The function parameters to be estimated are

Wage = a^o + b^o Age  if Age < 18

Wage = a¹ + b¹ Age  if 18 £ Age < 22

Wage = a² + b² Age if 22 £ Age

To implement this in a form that satisfies the continuity constraint and which is amenable to least squares let us define

The full model will be

The three slopes are

In order to ensure that the segments meet at the join points we must impose the following restrictions

This linear spline can be generalized in a couple of ways. First, the segments between the knots can be polynomials. Second, there can be more RHS variables with interactions. This has the effect of fitting planes with different gradients over the space spanned by the RHS variables.

An interactive look at dummy variables and splines.