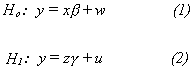
SPECIFICATION PROBLEMS: Part 4

Testing Non-nested Hypotheses
Suppose we have two alternative models that we are entertaining and wish to choose between them on statistical grounds. That is,

The models differ in the set of right hand side variables.
Define

Then the estimates of the error variances from the two specifications are

Suppose that model (1) is the truth. Then our estimate of the error variance of model two can be rewritten as

Upon taking expectations the middle term will drop out.

We can use a trick from our earlier examination of the unbiasedness of the error variance estimator. Namely, we will take the trace.

Substituting back

We can see that in expectation the estimated error variance of the incorrect model exceeds the error variance of the correct model. The question is whether we can detect this difference statistically. To do this we construct the statistic

What is the probability limit of this test statistic? By Slutsky's theorem we know that the probability limit of a function of a random variable is equal to the function of the probability limit of the random variable.

from (3) we can see that the numerator and the denominator are equal in the limit, so plim C₁₂ = 0.

and we can use the test statistic

There is a serious drawback to this test. Namely, it is not symmetric. We began by stating that (1) was the correct model and constructed a test statistic on this basis. If we begin by stating that (2) is the correct model and construct the test statistic then it is quite possible that we could reach a different conclusion. This is not the only time we encounter a conflict of criteria. It happens in the use of the LM, LR and Wald tests in finite samples. We also noted that using R² as a rule for variable inclusion is a bad idea since order matters.